Rethinking Multinomial Logistic Mixture of Experts with Sigmoid Gating Function

The sigmoid gate in mixture-of-experts (MoE) models has been empirically shown to outperform the softmax gate across several tasks, ranging from approximating feed-forward networks to language modeling. Additionally, recent efforts have demonstrated that the sigmoid gate is provably more sample-efficient than its softmax counterpart under regression settings. Nevertheless, there are three notable concerns that have not been addressed in the literature, namely (i) the benefits of the sigmoid gate have not been established under classification settings; (ii) existing sigmoid-gated MoE models may not converge to their ground-truth; and (iii) the effects of a temperature parameter in the sigmoid gate remain theoretically underexplored. To tackle these open problems, we perform a comprehensive analysis of multinomial logistic MoE equipped with a modified sigmoid gate to ensure model convergence. Our results indicate that the sigmoid gate exhibits a lower sample complexity than the softmax gate for both parameter and expert estimation. Furthermore, we find that incorporating a temperature into the sigmoid gate leads to a sample complexity of exponential order due to an intrinsic interaction between the temperature and gating parameters. To overcome this issue, we propose replacing the vanilla inner product score in the gating function with a Euclidean score that effectively removes that interaction, thereby substantially improving the sample complexity to a polynomial order.

A Statistical Theory of Gated Attention through the Lens of Hierarchical Mixture of Experts

Self-attention has greatly contributed to the success of the widely used Transformer architecture by enabling learning from data with long-range dependencies. In an effort to improve performance, a gated attention model that leverages a gating mechanism within the multi-head self-attention has recently been proposed as a promising alternative. Gated attention has been empirically demonstrated to increase the expressiveness of low-rank mapping in standard attention and even to eliminate the attention sink phenomenon. Despite its efficacy, a clear theoretical understanding of gated attention's benefits remains lacking in the literature. To close this gap, we rigorously show that each entry in a gated attention matrix or a multi-head self-attention matrix can be written as a hierarchical mixture of experts. By recasting learning as an expert estimation problem, we demonstrate that gated attention is more sample-efficient than multi-head self-attention. In particular, while the former needs only a polynomial number of data points to estimate an expert, the latter requires exponentially many data points to achieve the same estimation error. Furthermore, our analysis also provides a theoretical justification for why gated attention yields higher performance when a gate is placed at the output of the scaled dot product attention or the value map rather than at other positions in the multi-head self-attention architecture.

Low-Dimensional Adaptation of Rectified Flow: A New Perspective through the Lens of Diffusion and Stochastic Localization

In recent years, Rectified flow (RF) has gained considerable popularity largely due to its generation efficiency and state-of-the-art performance. In this paper, we investigate the degree to which RF automatically adapts to the intrinsic low dimensionality of the support of the target distribution to accelerate sampling. We show that, using a carefully designed choice of the time-discretization scheme and with sufficiently accurate drift estimates, the RF sampler enjoys an iteration complexity of order $O(k/\varepsilon)$ (up to log factors), where $\varepsilon$ is the precision in total variation distance and $k$ is the intrinsic dimension of the target distribution. In addition, we show that the denoising diffusion probabilistic model (DDPM) procedure is equivalent to a stochastic version of RF by establishing a novel connection between these processes and stochastic localization. Building on this connection, we further design a stochastic RF sampler that also adapts to the low-dimensionality of the target distribution under milder requirements on the accuracy of the drift estimates, and also with a specific time schedule. We illustrate with simulations on the synthetic data and text-to-image data experiments the improved performance of the proposed samplers implementing the newly designed time-discretization schedules.

On Minimax Estimation of Parameters in Softmax-Contaminated Mixture of Experts

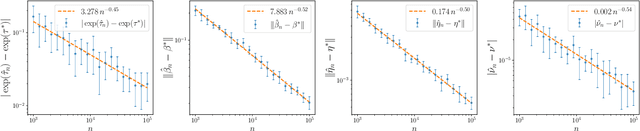
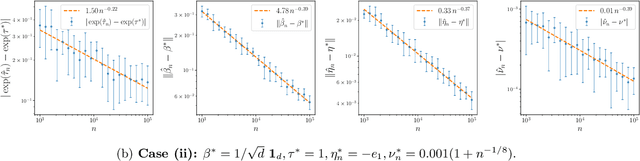
The softmax-contaminated mixture of experts (MoE) model is deployed when a large-scale pre-trained model, which plays the role of a fixed expert, is fine-tuned for learning downstream tasks by including a new contamination part, or prompt, functioning as a new, trainable expert. Despite its popularity and relevance, the theoretical properties of the softmax-contaminated MoE have remained unexplored in the literature. In the paper, we study the convergence rates of the maximum likelihood estimator of gating and prompt parameters in order to gain insights into the statistical properties and potential challenges of fine-tuning with a new prompt. We find that the estimability of these parameters is compromised when the prompt acquires overlapping knowledge with the pre-trained model, in the sense that we make precise by formulating a novel analytic notion of distinguishability. Under distinguishability of the pre-trained and prompt models, we derive minimax optimal estimation rates for all the gating and prompt parameters. By contrast, when the distinguishability condition is violated, these estimation rates become significantly slower due to their dependence on the prompt convergence rate to the pre-trained model. Finally, we empirically corroborate our theoretical findings through several numerical experiments.

On DeepSeekMoE: Statistical Benefits of Shared Experts and Normalized Sigmoid Gating

Mixture of experts (MoE) methods are a key component in most large language model architectures, including the recent series of DeepSeek models. Compared to other MoE implementations, DeepSeekMoE stands out because of two unique features: the deployment of a shared expert strategy and of the normalized sigmoid gating mechanism. Despite the prominent role of DeepSeekMoE in the success of the DeepSeek series of models, there have been only a few attempts to justify theoretically the value of the shared expert strategy, while its normalized sigmoid gating has remained unexplored. To bridge this gap, we undertake a comprehensive theoretical study of these two features of DeepSeekMoE from a statistical perspective. We perform a convergence analysis of the expert estimation task to highlight the gains in sample efficiency for both the shared expert strategy and the normalized sigmoid gating, offering useful insights into the design of expert and gating structures. To verify empirically our theoretical findings, we carry out several experiments on both synthetic data and real-world datasets for (vision) language modeling tasks. Finally, we conduct an extensive empirical analysis of the router behaviors, ranging from router saturation, router change rate, to expert utilization.

Convergence Rates for Softmax Gating Mixture of Experts

Mixture of experts (MoE) has recently emerged as an effective framework to advance the efficiency and scalability of machine learning models by softly dividing complex tasks among multiple specialized sub-models termed experts. Central to the success of MoE is an adaptive softmax gating mechanism which takes responsibility for determining the relevance of each expert to a given input and then dynamically assigning experts their respective weights. Despite its widespread use in practice, a comprehensive study on the effects of the softmax gating on the MoE has been lacking in the literature. To bridge this gap in this paper, we perform a convergence analysis of parameter estimation and expert estimation under the MoE equipped with the standard softmax gating or its variants, including a dense-to-sparse gating and a hierarchical softmax gating, respectively. Furthermore, our theories also provide useful insights into the design of sample-efficient expert structures. In particular, we demonstrate that it requires polynomially many data points to estimate experts satisfying our proposed \emph{strong identifiability} condition, namely a commonly used two-layer feed-forward network. In stark contrast, estimating linear experts, which violate the strong identifiability condition, necessitates exponentially many data points as a result of intrinsic parameter interactions expressed in the language of partial differential equations. All the theoretical results are substantiated with a rigorous guarantee.

Uncertainty quantification for Markov chains with application to temporal difference learning

Markov chains are fundamental to statistical machine learning, underpinning key methodologies such as Markov Chain Monte Carlo (MCMC) sampling and temporal difference (TD) learning in reinforcement learning (RL). Given their widespread use, it is crucial to establish rigorous probabilistic guarantees on their convergence, uncertainty, and stability. In this work, we develop novel, high-dimensional concentration inequalities and Berry-Esseen bounds for vector- and matrix-valued functions of Markov chains, addressing key limitations in existing theoretical tools for handling dependent data. We leverage these results to analyze the TD learning algorithm, a widely used method for policy evaluation in RL. Our analysis yields a sharp high-probability consistency guarantee that matches the asymptotic variance up to logarithmic factors. Furthermore, we establish a $O(T^{-\frac{1}{4}}\log T)$ distributional convergence rate for the Gaussian approximation of the TD estimator, measured in convex distance. These findings provide new insights into statistical inference for RL algorithms, bridging the gaps between classical stochastic approximation theory and modern reinforcement learning applications.

Statistical Inference for Temporal Difference Learning with Linear Function Approximation

Statistical inference with finite-sample validity for the value function of a given policy in Markov decision processes (MDPs) is crucial for ensuring the reliability of reinforcement learning. Temporal Difference (TD) learning, arguably the most widely used algorithm for policy evaluation, serves as a natural framework for this purpose.In this paper, we study the consistency properties of TD learning with Polyak-Ruppert averaging and linear function approximation, and obtain three significant improvements over existing results. First, we derive a novel sharp high-dimensional probability convergence guarantee that depends explicitly on the asymptotic variance and holds under weak conditions. We further establish refined high-dimensional Berry-Esseen bounds over the class of convex sets that guarantee faster rates than those in the literature. Finally, we propose a plug-in estimator for the asymptotic covariance matrix, designed for efficient online computation. These results enable the construction of confidence regions and simultaneous confidence intervals for the linear parameters of the value function, with guaranteed finite-sample coverage. We demonstrate the applicability of our theoretical findings through numerical experiments.

Straightness of Rectified Flow: A Theoretical Insight into Wasserstein Convergence

Diffusion models have emerged as a powerful tool for image generation and denoising. Typically, generative models learn a trajectory between the starting noise distribution and the target data distribution. Recently Liu et al. (2023b) designed a novel alternative generative model Rectified Flow (RF), which aims to learn straight flow trajectories from noise to data using a sequence of convex optimization problems with close ties to optimal transport. If the trajectory is curved, one must use many Euler discretization steps or novel strategies, such as exponential integrators, to achieve a satisfactory generation quality. In contrast, RF has been shown to theoretically straighten the trajectory through successive rectifications, reducing the number of function evaluations (NFEs) while sampling. It has also been shown empirically that RF may improve the straightness in two rectifications if one can solve the underlying optimization problem within a sufficiently small error. In this paper, we make two key theoretical contributions: 1) we provide the first theoretical analysis of the Wasserstein distance between the sampling distribution of RF and the target distribution. Our error rate is characterized by the number of discretization steps and a new formulation of straightness stronger than that in the original work. 2) In line with the previous empirical findings, we show that, for a rectified flow from a Gaussian to a mixture of two Gaussians, two rectifications are sufficient to achieve a straight flow. Additionally, we also present empirical results on both simulated and real datasets to validate our theoretical findings.

Sigmoid Gating is More Sample Efficient than Softmax Gating in Mixture of Experts

The softmax gating function is arguably the most popular choice in mixture of experts modeling. Despite its widespread use in practice, softmax gating may lead to unnecessary competition among experts, potentially causing the undesirable phenomenon of representation collapse due to its inherent structure. In response, the sigmoid gating function has been recently proposed as an alternative and has been demonstrated empirically to achieve superior performance. However, a rigorous examination of the sigmoid gating function is lacking in current literature. In this paper, we verify theoretically that sigmoid gating, in fact, enjoys a higher sample efficiency than softmax gating for the statistical task of expert estimation. Towards that goal, we consider a regression framework in which the unknown regression function is modeled as a mixture of experts, and study the rates of convergence of the least squares estimator in the over-specified case in which the number of experts fitted is larger than the true value. We show that two gating regimes naturally arise and, in each of them, we formulate identifiability conditions for the expert functions and derive the corresponding convergence rates. In both cases, we find that experts formulated as feed-forward networks with commonly used activation such as $\mathrm{ReLU}$ and $\mathrm{GELU}$ enjoy faster convergence rates under sigmoid gating than softmax gating. Furthermore, given the same choice of experts, we demonstrate that the sigmoid gating function requires a smaller sample size than its softmax counterpart to attain the same error of expert estimation and, therefore, is more sample efficient.